Processing 麻柄
- NUM

- 2025年2月18日
- 読了時間: 7分
目次
はじめに
こんにちは。NUMです。
最近、BYOD^2というデジタルデータを物理空間に「インストール」するというコンセプトの展示会に参加しました。僕は現地に行けなかったですが、世界中からデジタルアートが集まって良い意味でカオスな空間を作り出す素晴らしい展示会だったそうです。 僕もYoutubeの配信を見ていましたがジェネラティブアートは結構展示の場がないので、このような機会を作ってくださったNEORTさんには感謝しかないです。
今回は日本を代表する和柄である「麻柄」について書いていきます。 僕は日本人ということもあり、自身の作品に和のテイストを取り入れるきっかけにもなり、 意外と和柄を作ったことがなく、今回を機に色んな和柄に挑戦していきたいと思います。
麻柄の歴史

六角形を用いたパターンは、古くから日本の伝統模様である「麻柄」として使われてきました。 麻柄は、麻の葉の形を模した幾何学模様で、規則正しく六角形が並ぶデザインが特徴です。
麻は成長が早く丈夫な植物であるため、古くから着物や装飾に用いられ、麻柄には「健やかな成長」や「魔除け」の意味が込められています。 特に、子供の産着や神社仏閣の装飾に多く使われ、日本の美意識を象徴するパターンのひとつです。この麻柄の構造は、数学的にも美しい幾何学的配置を持ち、現代のデザインやコンピュータグラフィックスにも活かされています。
六角形の特徴
正六角形は、辺、角が全て等しい特徴を持つ正多角形であり、以下の特性を持ちます。
内角の和 | 720° |
1つの内角 | 120° |
対称性 | 回転対称性(60°ずつ回転しても同じ形) 鏡映対称性(各辺を軸とした対称性) |
円との関係 | 正六角形は円に内接する形をしており、円の半径をrとした場合、六角形の各辺の長さもrになる |
このように充填しやすい形のため、建築、数学、自然界(蜂の巣など)でもよく登場します。
充填ルール
六角形の充填ルールは偶数行、奇数行で移動量が異なります。 偶数行の場合、x座標を基準位置とするためy方向の移動のみとします。奇数行の場合、二つの六角形の間に配置が必要なため、x、y方向それぞれ移動を行います。

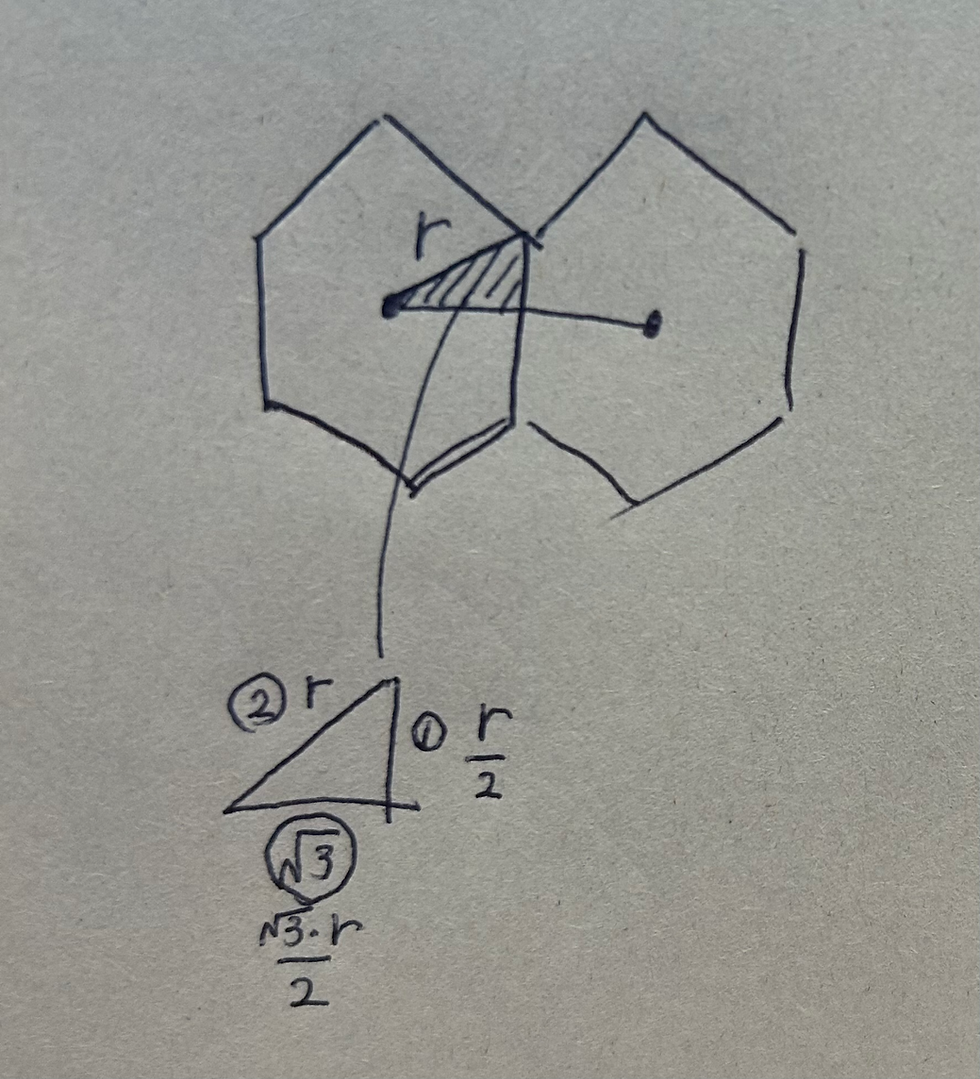
水平方向の移動量 | 水平方向の移動距離は中心から頂点までをrとすると、三平方の定理の√3の部分の長さになります。 |
垂直方向の移動量 | 六角形をズレながら並べるため、奇数行の六角形は隙間を埋めるように配置されます。そのため、各六角形の縦方向の移動量は六角形の高さの半分 + 六角形の半分の高さ となります。 つまり、 1.5 × r となります。 |
実装
プログラム概要は以下3つとなります。
六角形を6つの三角形で構成
三角形の頂点から重心に線を引く
六角形を適切な移動量で敷き詰める
void setup() {
size(850, 850);
background(255);
pixelDensity(displayDensity());
fill(255, 0, 0);
linenPattern(100);
}
/**
* 六角形を格子状に配置する。
* @param r 六角形の外接円の半径
*/
void linenPattern(int r) {
int maxY = height / r;
int maxX = width / r;
float addX = (sqrt(3) * r) / 2; // 水平方向の移動量
float addY = r * 1.5; // 垂直方向の移動量
// 垂直方向の移動量は一定、水平方向は奇数行のみaddX分ずらす
for (int i = 0; i < maxX; i++) {
for (int j = 0; j < maxY; j++) {
float x = i * addX * 2;
float y = j * addY;
// 奇数行は x 座標をオフセット
if (j % 2 == 1) {
x += addX;
}
hexagon(x, y, r);
}
}
}
/**
* 指定した座標に六角形を描画する。
* 六角形を三角形に分割し、各三角形の重心を求める。
* @param x 六角形の中心のX座標
* @param y 六角形の中心のY座標
* @param r 六角形の外接円の半径
*/
void hexagon(float x, float y, float r) {
float prevX = x + r * cos(radians(30));
float prevY = y + r * sin(radians(30));
//三角形を6つ配置して六角形を作成
for (float ang = 90; ang <= 390; ang += 60) {
float nextX = x + r * cos(radians(ang));
float nextY = y + r * sin(radians(ang));
centroidTriangle(x, y, prevX, prevY, nextX, nextY);
prevX = nextX;
prevY = nextY;
}
}
/**
* 三角形を描画し、その重心から各頂点へ線を引く。
* @param x1 三角形の頂点1のX座標
* @param y1 三角形の頂点1のY座標
* @param x2 三角形の頂点2のX座標
* @param y2 三角形の頂点2のY座標
* @param x3 三角形の頂点3のX座標
* @param y3 三角形の頂点3のY座標
*/
void centroidTriangle(float x1, float y1, float x2, float y2, float x3, float y3) {
// 重心の座標計算
float centroidX = (x1 + x2 + x3) / 3;
float centroidY = (y1 + y2 + y3) / 3;
stroke(0);
triangle(x1, y1, x2, y2, x3, y3); // 三角形の描画
// 三角形の頂点から重心に線を引く
line(centroidX, centroidY, x1, y1);
line(centroidX, centroidY, x2, y2);
line(centroidX, centroidY, x3, y3);
}
それではプログラムを理解する上で重要な点のみ説明していきます。
void hexagon(float x, float y, float r) {
float prevX = x + r * cos(radians(30));
float prevY = y + r * sin(radians(30));
//三角形を6つ配置して六角形を作成
for (float ang = 90; ang <= 390; ang += 60) {
float nextX = x + r * cos(radians(ang));
float nextY = y + r * sin(radians(ang));
centroidTriangle(x, y, prevX, prevY, nextX, nextY);
prevX = nextX;
prevY = nextY;
}
}
上記は六角形を作成するプログラムですが、麻柄を作成することが目的なので、六角形は三角形を敷き詰めて作成しています。そのため普通に六角形を作成するプログラムに比べると違和感があると思います。

三角形を敷き詰めていくには3つの頂点が必要で、ループ開始時は中心点、30°、90°の頂点を使用して三角形を作成しています。(白色の三角形) 次回ループは前回のnextX、Yの値をprevに代入し、新しい角度の値をnextで使用します。 中心点は常に同じなので、prevとnextを計算するだけで良いというわけです。

三角形の中心座標は以下の重心公式で求めることができます。

重心が求められたら各頂点から線を引いていきます。
void centroidTriangle(float x1, float y1, float x2, float y2, float x3, float y3) {
// 重心の座標計算
float centroidX = (x1 + x2 + x3) / 3;
float centroidY = (y1 + y2 + y3) / 3;
stroke(0);
triangle(x1, y1, x2, y2, x3, y3); // 三角形の描画
// 三角形の頂点から重心に線を引く
line(centroidX, centroidY, x1, y1);
line(centroidX, centroidY, x2, y2);
line(centroidX, centroidY, x3, y3);
}
六角形の充填処理は充填ルールのセクションで説明した水平方向、垂直方向の移動が重要になってきます。
void linenPattern(int r) {
int maxY = height / r;
int maxX = width / r;
float addX = (sqrt(3) * r) / 2; // 水平方向の移動量
float addY = r * 1.5; // 垂直方向の移動量
// 垂直方向の移動量は一定、水平方向は奇数行のみaddX分ずらす
for (int i = 0; i < maxX; i++) {
for (int j = 0; j < maxY; j++) {
float x = i * addX * 2;
float y = j * addY;
// 奇数行は x 座標をオフセット
if (j % 2 == 1) {
x += addX;
}
hexagon(x, y, r);
}
}
}
六角形の大きさrを考慮したループ最大値maxX,Yと水平、垂直方向の移動量を事前に計算しています。ループ内で値が変化しないものはループ外で計算しておくとパフォーマンスが良くなります。
int maxY = height / r;
int maxX = width / r;
float addX = (sqrt(3) * r) / 2; // 水平方向の移動量
float addY = r * 1.5; // 垂直方向の移動量
水平、垂直方向をループ変数で計算します。
float x = i * addX * 2; // 水平方向は2倍
float y = j * addY; // 垂直方向は一定
内側ループはまず縦方向に描画していきます。 以下コードは奇数行の場合はx座標をずらして六角形の隙間を埋めていくための処理です。
// 奇数行は x 座標をオフセット
if (j % 2 == 1) {
x += addX;
}

まとめ
今回はProcessing を使って六角形グリッドを描画する方法を紹介しました。六角形の配置にはx、y方向の移動量を正しく計算することで規則正しく並べることができます。 また、日本の伝統模様である麻柄についても紹介しました。この記事を読んで和柄に挑戦してみるきっかけになれば嬉しいです。

最後まで読んでいただきありがとうございました!




コメント